top of page

PROYECTO: TRIÁNGULOS

¿Cómo se clasifican los triángulos?

Hay varios criterios de clasificación, pero estos son los más importantes.

CLASIFICACIÓN DE TRIÁNGULOS
Según sus lados
Según sus ángulos
Según sus ángulos

RETO 1:

El esquema anterior, como has podido ver, está incompleto. Tu primera misión será completarlo. 

​

Para ello, tienes que buscar en internet la clasificación de triángulos según sus lados y la clasificación de triángulos según sus ángulos y ampliar el esquema. Incluye también fotografías de dichos tipos de triángulos.

​

Utiliza la aplicación GoConqr. Créate una cuenta si no la tienes ya. Es muy sencilla de utilizar. Entra en la opción "Crear" y después en "Mapa mental".

​

Cuando lo tengas terminado, descarga el mapa mental o haz una captura de pantalla y súbelo a tu portafolio. Antes, crea una portada en la que ponga "Proyecto final: triángulos".

Los triángulos rectángulos

Son aquellos en los que uno de los 3 ángulos es recto, es decir, mide 90º.

Como vemos en la imagen, a los lados que forman el ángulo recto se les llama catetos y al lado largo hipotenusa.

RETO 2:

Realiza el siguiente puzzle donde podrás encontrar diferentes tipos de triángulos.

Pulsando sobre la opción del fantasma podrás ver una imagen de ayuda para resolverlo más fácilmente.

Una vez resuelto:

        - Sube una captura de pantalla a tu portafolio.

        - Crea y completa una tabla en tu portafolio como la siguiente, rellenando los huecos para cada triángulo según al grupo que pertenezca:

​

​

El teorema de Pitágoras

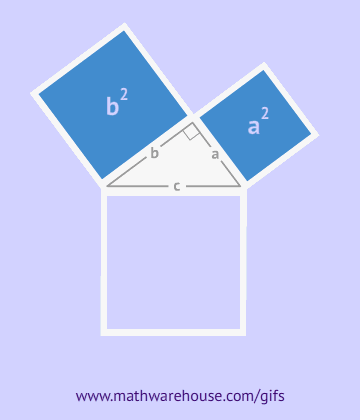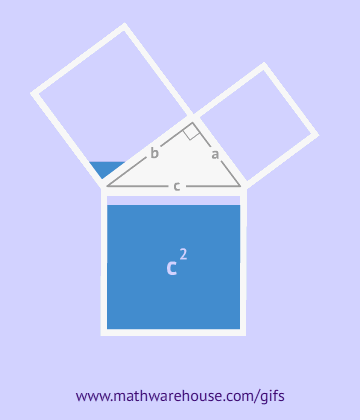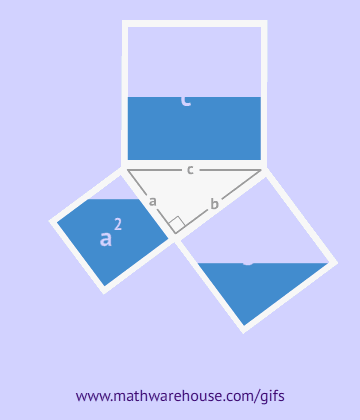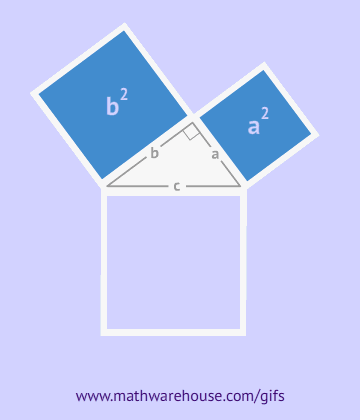
Hace mucho tiempo, el matemático griego Pitágoras descubrió una propiedad interesante de los triángulos rectángulos, y es que si calculas el área de un cuadrado que tiene por lado la hipotenusa del triángulo, el resultado es la suma de las áreas de dos cuadrados que tienen por lados los dos catetos. 

Si echas un vistazo a los siguientes GIFs, podrás comprender mejor esta propiedad:

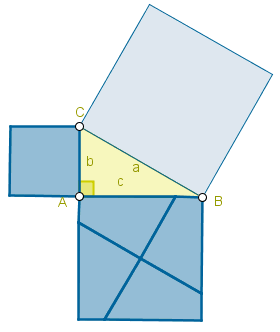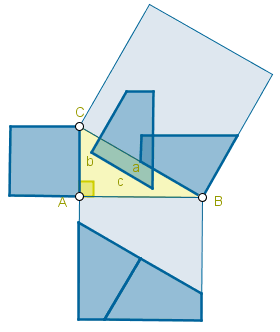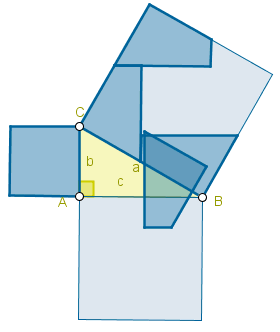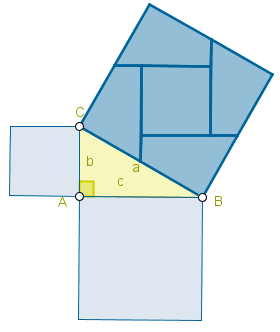
RETO 3:

Dibuja en tu portafolio, con las herramientas de dibujo,  el siguiente triángulo:

h = 13 cm

a = 5 cm

b = 12 cm

Dibuja 3 cuadrados, uno apoyado en el cateto a del triángulo, otro apoyado en el cateto b del triángulo y otro apoyado en la hipotenusa h.

​

Calcula el área de los 3 cuadrados (si no recuerdas la fórmula para calcular el área de un cuadrado, búscala en internet)

​

Comprueba que la suma del área de los dos cuadrados pequeños (los formados por los catetos a y b) es igual a la suma del cuadrado grande (formado por la hipotenusa h)

​

¡ENHORABUENA! ACABAS DE DEMOSTRAR EL TEOREMA DE PITÁGORAS

Cálculos pitagóricos

RETO 4:

h
a
b

Cada uno de los siguientes cuadrados está dividio a su vez por otros cuadrados más pequeños de superficie 1cm cuadrado.

​

Si la superficie del cuadrado rojo es 25cm cuadrados, responde (no olvides subir la fotografía anterior al portafolio, ponla en la misma diapositiva que las respuestas).

​

PREGUNTA 1: ¿Cuál será la superficie del cuadrado verde? ¿Y la del cuadrado azul?

​

PREGUNTA 2: ¿Se cumple el teorema de Pitágoras? Demuéstralo.

​

PREGUNTA 3: ¿Cuál sería el valor, en centímetros, de la hipotenusa "h"? ¿Y de los catetos "a" y "b"? 

​

​

La fórmula matemática del teorema de Pitágoras

Ahora que ya entendemos la demostración del teorema de Pitágoras, es hora de empezar a utilizar su fórmula matemática.

​

¡Es muy fácil! Si te fijas, todo parte de la demostración gráfica del teorema con las áreas de los cuadrados formados por cada lado del triángulo rectángulo.

a
b
h
b
a
h

Si la hipotenusa es "h", el área del cuadrado rojo será: h 

2

Si el cateto pequeño es "a", el área del cuadrado azul será: a

2

Si el cateto pequeño es "b", el área del cuadrado verde será: b

2

Por tanto, como el área del cuadrado rojo tiene que ser la suma de las áreas de los cuadrados verde y azul, nos queda la siguiente expresión:

h = a + b

2
2
2

RETO 5:

De los siguientes valores de triángulos, comprueba cuáles cumplen el teorema de Pitágoras y cúales no:

​

CASO 1: a=3   b=4    h=5

​

CASO 2: a=5  b=12   c=13

​

CASO 3: a=4   b=6   c=12

​

CASO 4: a=7   b=24   c=25

El teorema de Pitágoras nos sirve para conocer el valor de un lado de un triángulo rectángulo si conocemos los otros dos.

Por ejemplo, en el siguiente caso queremos calcular la longitud del hilo de una cometa atada a un poste de 6m de altura, si sabemos que el poste está a 50 metros de distancia de nosotros.

​

En este caso la hipotenusa, "h", sería la longitud del hilo, el cateto pequeño, "a" sería la altura del poste y el cateto grande, "b", sería la distancia de la persona al poste.

h
b
a

Para calcular la distancia, h, aplicamos lo que ya conocemos del teorema de Pitágoras​

​

h = a + b

2
2
2

h = 6 + 50

2
2
2

h = 36 + 2500 = 2536 

2

Para calcular el valor de "h" tenemos que sacar la raíz cuadrada del resultado:

h =     2536 = 50,36m 

RETO 6:

Calcula el valor de la hipotenusa "h" para los siguientes valores de catetos de triángulos rectángulos:

 

CASO 1: a = 10   b = 15

 

CASO 2: a = 16   b = 30

 

CASO 3: a = 3    b = 12

 

CASO 4: a = 11   b = 60 

¿Cómo calculamos el valor de uno de los catetos si conocemos el valor del otro cateto y de la hipotenusa?

¡Muy sencillo! Solo tienes que despejar el valor de ese cateto en la fórmula del teorema de Pitágoras.

Cálculo del cateto "a"

Cálculo del cateto "b"

h = 13 cm

a = ?

b = 12 cm

h = a + b

2
2
2
2

a = h - b

2
2

a =   h - b

2
2

a =   13 - 12 =5 cm 

2
2

a = 5

h = 13 cm

b = ?

h = a + b

2
2

b = h - a

2
2
2

Esta operación se resolverá en el reto 7

RETO 7:

Calcula el valor de los catetos para los siguientes valores de lados de triángulos rectángulos:

 

CASO 1: calcula el valor del cateto "b" en el ejempo de teoría anterior que está sin resolver.

​

CASO 2: a = ?   b = 30   h = 42

 

CASO 3: a = 12    b = ?  h = 37

​

CASO 4: a = ?   b = 15   h = 17

 

CASO 5: a = 13  b = ?   h = 85 

RETO 8:

ENTRA EN LA SIGUIENTE WEB Y PÍDELE A TU PROFESOR QUE TE DE EL CÓDIGO PARA UNIRTE A LA ACTIVIDAD.

​

​

WEB

bottom of page